2025-03-03 graphs lecture 11
[[lecture-data]]
1. Graph Signals and Graph Signal Processing
Recall from last time that injective GNNs are as powerful as the WL test:
A graph isomorphism network (GIN) layer is defined as
We can write this layer in terms of concatenate function
And aggregate function
The motivation for this architecture comes from the fact that injective GNNs are as powerful as the WL test, which holds in this case as long as
Here,
- Hornik 1989 says an MLP can model any injective function - this is due to the universal approximation theorem
- Injective
exist for multiset (proven in paper where GINs are introduced)
Can we map an injective function from multisets to embeddings using composition?
- Yes, using one-hot encoding of multisets
- The function/parameterization is such that it is possible to learn
- Original graph isomorphism paper added to the Canvas
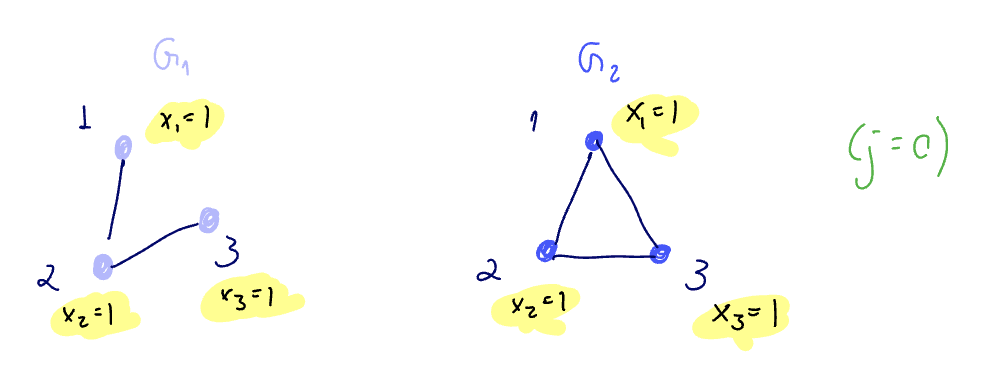
Can a GIN tell them apart? We assume
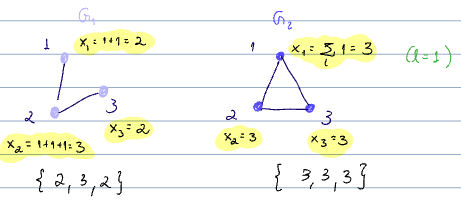
- output is
- output is
As long as we have an injective function from multisets to embeddings, we are OK since we will be able to distinguish between these. To confirm we have this, we look at the graph level readout.
In the GIN paper, the readout is defined in terms of a readout at each layer.
For the example above,
And so
thus, a GIN is a maximally powerful GNN in graph-level tasksfor anonymous inputs (ie
see GINs are maximally powerful for anonymous input graphs
Is being as powerful as the WL test enough?
Can WL test distinguish between the two graphs below?
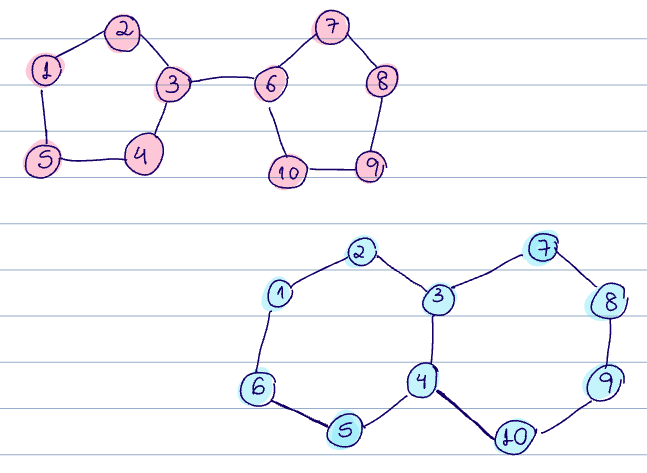
The output of the color refinement algorithm for Graph 1 gives:
- 1, 2, 3, 4, 5, 7, 8, 9, 10 have color 1
- 3, 6 have color 2
And for Graph 2:
- 1,2,5,6, 7,8,9,10 have color 1
- 3,4 have color 2
So in this case, the multisets of the colors are the same between G1 and G2, and we cannot distinguish between them.
So, NO! Thus, the computational graphs are the same, despite these being different graphs.
Check
Instead, we could count the number of cycles to see if these graphs are different.
- 2 cycles in graph1
- 3 cycles in graph2
But GNNs are less powerful than the WL test, so GNNs could not discriminate between these graphs. And this implies that they cannot count cycles.
There is another way to count cycles: densities of cycle homomorphisms
Let
ie, homomorphisms are adjacency-preserving maps (of
How is a homomorphism not the same as a graph isomorphism?
Recall the definition of the isomorphism
The isomorphism requires that both graphs share all edges. The homomorphism requires that the second graph,
, is a subgraph of the first, .
Example
+++see notes
A valid homomorphism is
We will denote the total number of homomorphisms from
Let
Where
Let
For
Where
Note that
Thus
This implies that cycles can be counted using a convolutional GNN with white input (see Lecture 9) with graph shift operator
see cycle homomorphism density is given by the trace of the adjacency matrix
This is similar to We can verify whether graphs without node features and different laplacian eigenvalues are not isomorphic
- we can set
to be 1 for the nodes we want in the cycle
+++note/distill how to get the cycle density using this type of algorithm
To be able to count these cycles, we need the input to be white. For the GIN, we needed to have the inputs to be anonymous ie each
For this method to work, we need each
This means that white inputs help improve expressivity (as opposed to anonymous inputs
The "best of both worlds" can be achieved by merging the two methods: using a GIN with white inputs
Since designing a white inputs requires computing eigendecomposition, we usually relax this condition to random inputs instead, which almost surely satisfy
For maximum expressivity, we can use a GIN with white, anonymous inputs. That is,
- Each
- Each
However, designing a white inputs requires computing eigendecomposition which is expensive.
Instead, we usually relax this condition to random inputs, which almost surely satisfy
see random graphs in a gin are good for graph isomorphism
TBC in HW2
Detour:
- properties of GNNs
- permutation equiv
- expressivity
- limitations/advantages of conv archs
- Next:
- stability to perturbations
Detour:
- implementations in
PyTorch Geometric
see lecture 11 notebook
torch_geometric
- graphs no longer represented as adjacency matrices
- something similar to sparse matrix representations
Node features represented as
to_networkx from torch_geometric.utils
to convert to networkx object to plot :)
In general, going to use benchmark datasets
- citation network, classify into communities
see notebook for defining a GNN in pyG - have layers implemented already