2025-02-05 graphs lecture 5

Data

subject:: Data Science Methods for Large Scale Graphs

2025-02-05

Table of Contents

Summary

Housekeeping

Scribing

Last Time

graph convolutions and design
Learning weights of graph convolution
Empirical risk minimization problem, statistical risk minimization problem
3 problems
- graph-level problem
- node-level task / inductive learning

Today

Graph Neural Networks
- graph perceptron
- multi-layer graph perceptron
- PyTorch (HW) FC NN

1. Graph Signals and Graph Signal Processing

Graph filters work ok for many things, but are limited to linear representations. Therefore, they lack expressivity if the task is complicated. ie, since these operations are only linear, we not able to represent more complex relationships.

Thus, we need to add nonlinearities (ex. ReLU etc) to help with the expressivity of our model. These techniques have been implemented in CNNs for image processing and other domains. GNNs will extend the ideas seen in CNNs to the graph domain - graph convolution .

Simple CNN

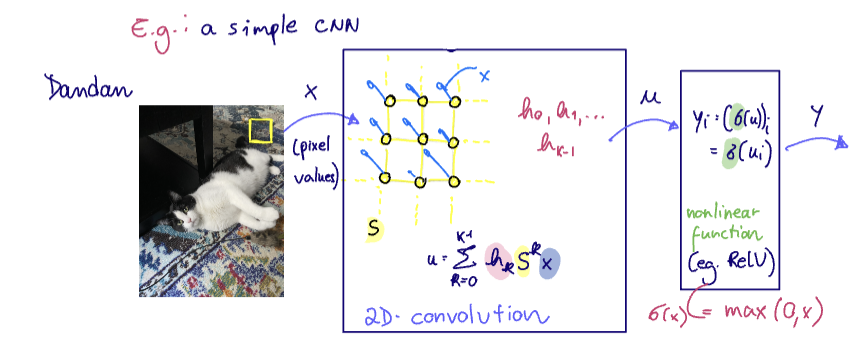
We can also think of any image as a graph, where the graph signals are the RGB values at each pixel, and the graph structure is determined by the pixel layout/grid of the image.

Graph Perceptron

Let $σ : R \to R$ . The graph perceptron is defined as

\begin{aligned} x \in R^{n} & \to u = \sum_{k = 0}^{K - 1} h_{k} S^{k} x graph conv \to_{u} \\ \to_{u} y \cdot σ (u) pointwise nonlinearity \to_{y} \end{aligned}

ie a graph convolution followed by a pointwise nonlinear function

y_{i} = σ (u_{i})

Examples

$σ (x) = max (0, x)$ ReLU
$σ (x) = \frac{1}{1 + e^{- x}}$ Sigmoid
$σ (x) = \tanh (x) = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}$ hypertangent

(see graph perceptron)

Question

Is a graph perceptron local?

Answer

Yes, we can still write the perceptron in terms of the local nodes, since convolutional graph filters are local

Multi-Layer Graph Perceptron

A(n $ℓ$ -layer) multi-layer graph perceptron (MGLP) is simply several graph perceptrons in sequence. This forms a function with input $x_{0} = x$ , and output $y = x_{L}$ .

Where at each layer, $$x_{\ell} = \sigma(u_{\ell}) = \sigma\left( \sum_{k=0}^{K-1} h_{\ell,k} S^k x_{\ell-1} \right), ; 1 \leq \ell \leq L$$
We call $x_{ℓ}$ the $ℓ$ -layer embedding.

For conciseness, we define our weights $H = {h_{k, ℓ} | 0 \leq k \leq K - 1, 1 \leq ℓ \leq L}$ and represent our MLGP as $$y = \Phi(x, S; H)$$

Illustration

(see multi-layer graph perceptron)

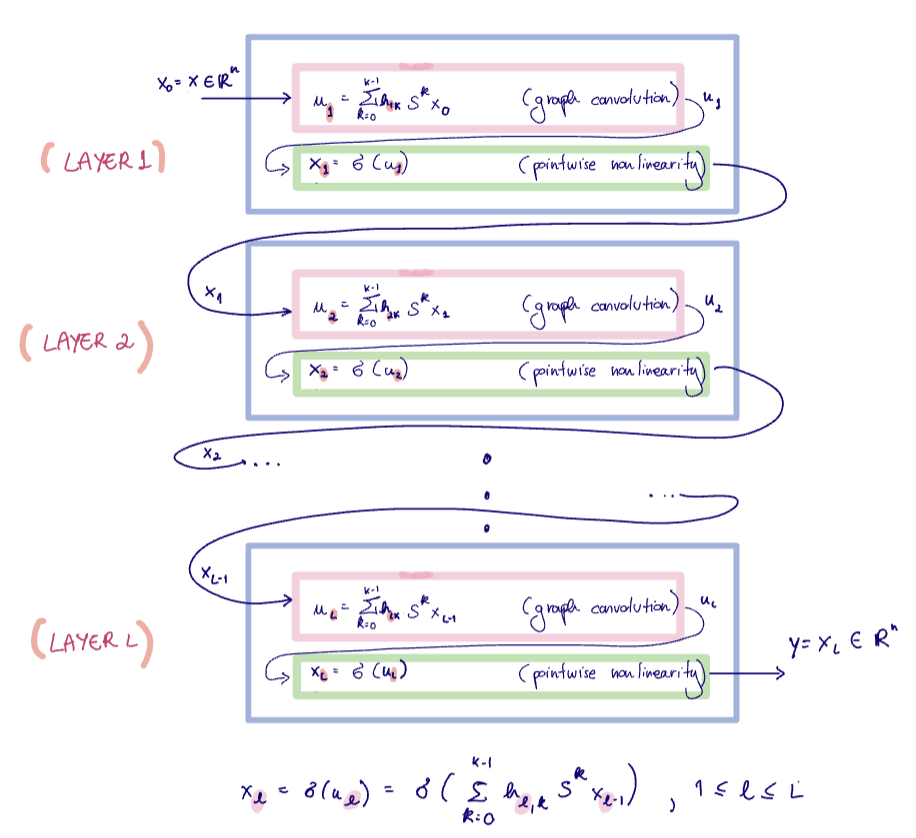
Full-Fledged GNNs

Real-world graph data is often high dimensional.

in addition to having signal values at the nodes, we often have many features. That is, our signal $x \in R^{n \times d}$ where $n$ is the number of nodes and $d$ is the number of features
(previously we have been looking at the case where $d = 1$ )
Thus it will be necessary for the embeddings $x_{ℓ}$ to be multi-dimensional. Note that we also may want embeddings to be multi-dimensional for higher expressivity/flexibility/better representations, not solely because it is necessary.

Example

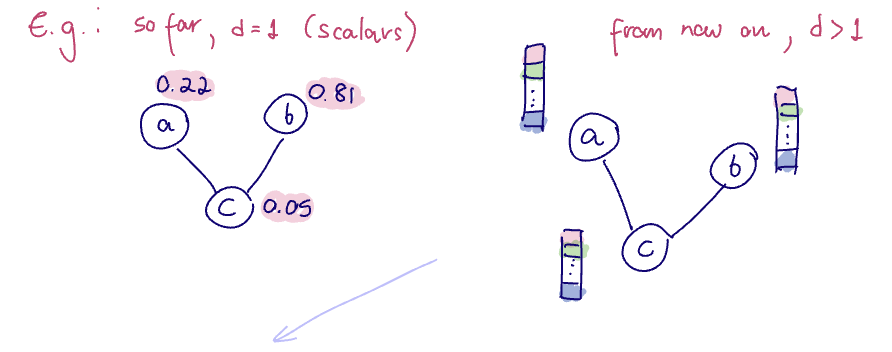
Suppose $a, b, c$ are drones communicating via wifi and $x$ is their spatial coordinate in 3D: $x \in R^{3 \times 3}$ .

In order to do this, we need graph convolution that take in multi-dimensional data.

Convolutional Filter Bank

Let $X \in R^{n \times d}$ , $H_{k} \in R^{d \times d^{'}}$ for $k = 0, \dots, K - 1$ . Then a convolutional filter bank (or multiple input multiple output graph convolution) is a multi-dimensional graph convolutiongiven by

Y = \sum_{k = 0}^{K - 1} S^{k} X H_{k}

$S^{k} \in R^{n \times n}$ is still a graph diffusion/shift
$H_{k}$ is a linear transformation mapping $d$ features to $d^{'}$ features

(see convolutional filter bank)

GNN

A "full-fledged" GNN layer is given by

X_{ℓ} = σ (u_{ℓ}) = σ (\sum_{k = 0}^{K - 1} S^{k} X_{ℓ - 1} H_{ℓ, k})

$H_{ℓ, k} \in R^{d_{ℓ - 1} \times d_{ℓ}}$ for $1 \leq ℓ \leq L$ , where

$X_{0} = X \in R^{n \times d_{0}}$
$Y = X_{L} \in R^{n \times d_{ℓ}}$

Here, $X_{ℓ}$ is still called an $ℓ$ -layer embedding.

(see Graph Neural Networks)

3 problems

1. Graph Signals and Graph Signal Processing

Full-Fledged GNNs