Weisfeiler-Leman Graph Isomorphism Test

[[concept]]

The Weisfeiler-Leman graph isomorphism test consists of running the color refinement algorithm for two graphs.

Motivation

Since the eigenvalue-based heuristic doesn't work for some graphs, a simple heuristic that does work is counting degrees. Then the problem amounts to comparing the multisets of node degree counts.

If the outputs of the algorithm are not the same, then the two graphs are not isomorphic.

Caution

If the outputs of the algorithm for the two graphs are the same, this is not an indicator that the two graphs are isomorphic! It means the test is inconclusive

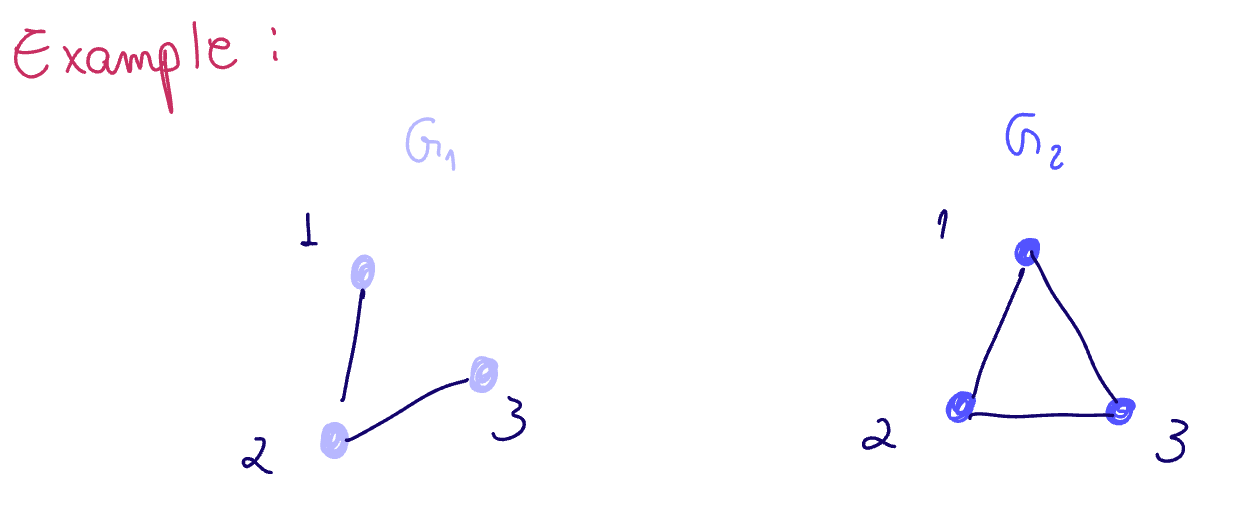
In this example, the two graphs have different outputs. Thus, we may conclude that they are not isomorphic.

Example

Color refinement for

G_{1}

No node features, so assume all 1. First, Assign colors based on node features.

step $t = 0$ :
$c_{1} (0) = c_{2} (0) = c_{3} (0) = f (\cdot, 1) = k_{1}$

step $t = 1$ :
$\begin{aligned} c_{1} (1) & = f (k_{1}, {k_{1}}) & = k_{1} \\ c_{3} (1) & = f (k_{1}, {k_{1}}) & = k_{1} \\ c_{2} (1) & = f (k_{1}, {k_{1}, k_{1}}) & = k_{2} \end{aligned}$
Evaluate: did the colors change?

Yes: continue!

step $t = 2$ :
$\begin{aligned} c_{1} (2) & = f (k_{1}, {k_{1}}) & = k_{1} \\ c_{3} (2) & = f (k_{1}, {k_{1}}) & = k_{1} \\ c_{2} (2) & = f (k_{2}, {k_{1}, k_{1}}) & = k_{2} \end{aligned}$
Evaluate: did the colors change?

No - so we are done!
This is the final coloring.

return ${k_{1}, k_{1}, k_{2}}$

Color refinement for

G_{2}

Again, there are no node features, so we assume the signals are all $1$ .

step $t = 0$ : assign colors based on node features:
$c_{1} (0) = c_{2} (0) = c_{3} (0) = f (\cdot, 1) = k_{1}$
step $t = 1$ :
$\begin{array}{r} c_{1} (1) = c_{2} (1) = c_{3} (1) = f (\cdot, {k_{1}, k_{1}}) = k_{1} \end{array}$

evaluate: did the colors change?

No - so we are done
This is the final coloring

return ${k_{1}, k_{1}, k_{1}}$

Mentions

File
graph isomorphism
injective GNNs are as powerful as the WL test
the WL test is at least as powerful as a GNN for detecting graph non-isomorphism
2025-02-19 graphs lecture 9
2025-02-24 graphs lecture 10
2025-03-03 graphs lecture 11
2025-03-05 graphs lecture 12
2025-02-25 equivariant lecture 4
2025-03-04 equivariant lecture 6