Given a graphon convolution with input graphon signal $\mathcal{X}$ and output $\mathcal{Y}$, the WFTs $\hat{\mathcal{X}}$ of $\hat{\mathcal{Y}}$ are related as

Where $h({\lambda }_j)=\sum _{k=0}^{K-1}{h}_k{\lambda }_j^k$ is our polynomial. Here, ${\hat{T}}_H$ acts pointwise on the graphon signal $\mathcal{X}$

• graphon convolutions act pointwise in the spectral domain

$$\begin{array}{rl}\mathcal{Y}& =\sum _{k=0}^{K-1}{h}_k\sum _{j\in \mathbb{Z}\setminus \{0\}}{\lambda }_j^k{\phi }_j(v)\underset{{\hat{x}}_j}{\underbrace{{\int }_0^1{\phi }_j(u)\mathcal{X}(u)du}}\\ & =\sum _{k=0}^{K-1}{h}_k\sum _{j\in \mathbb{Z}\setminus \{0\}}{\lambda }_j^k{\phi }_j(v)\hat{\mathcal{X}}\\ ⟹{\hat{\mathcal{Y}}}_i& ={\int }_0^1\mathcal{Y}(u){\phi }_i(u)du\\ & =\sum _{k=0}^{K-1}{h}_k{\lambda }_i^k{\cancel{\int {\phi }_i^2(u)du}}^1{\hat{x}}_i\\ ⟹{\hat{\mathcal{Y}}}_i& =\sum _{k=0}^{K-1}{h}_k{\lambda }_i^k{\hat{x}}_i\end{array}$$

This is a simple result following the diagonalization of $T_W^{(k)}$ by ${\phi }_i$

Some interesting takeaways (analogues of the graph convolution)

• Like the WFT, the spectral response of a graphon convolution is discrete
• the $j$th spectral component of the output $\mathcal{Y}$ only depends on ${\lambda }_j$ and spectral graphon signal ${\hat{\mathcal{X}}}_j$
  • ie ${\hat{\mathcal{Y}}}_j$ depends only on ${\lambda }_j$ and ${\hat{\mathcal{X}}}_j$
• The spectral response of $T_H$ given by $h(\lambda )=\sum _{k=0}^{K-1}{h}_k{\lambda }^k$ is independent of the underlying $W$ (like the spectral response of $H(S)$ was independent of the graph)
• ie, the spectral response can be written as a polynomial function. The eigenvalues of the graphon determine where we evaluate this function. (samples of function that is eigenvalues/spectrum)

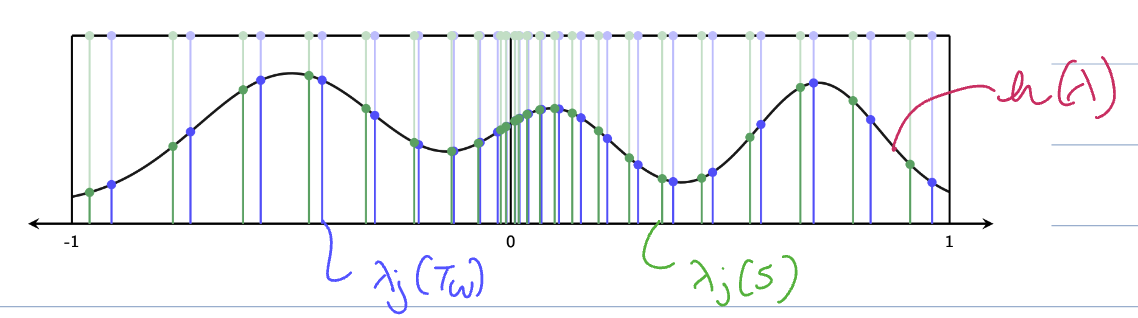
Sampling eigenvalues from the spectrum polynomial

Given the same (fixed) coefficients $h_k$, define the graph convolution $H(S)x=\sum _{k=0}^{K-1}{h}_k{S}^{k}x$. The spectral representation of that convolution is $h(\lambda )=\sum _{k=0}^{K-1}{h}_k{\lambda }^k$

• this is the same as the spectral representation of graphon convolutions/function for the same coefficients.
• The only difference is where the function is evaluated.
  • For a graphon, we evaluate it at the graphon shift operator eigenvalues ${\lambda }_j(T_W)$ for graphon signal $T_{H_j}$
  • For a graph, this is the graph shift operator eigenvalues ${\lambda }_j(S)$ for the graph signal $H(S{)}_j$