spectral representation of a convolutional graph filter

in the spectral/frequency domain, we have

this representation is completely defined by the polynomial $h(\lambda )=\sum _{k=0}^{K-1}{h}_k{\lambda }^k$
^representation

The spectral representation/frequency response of $H(S)$ is

^response

Because the spectral representation of a graph filter is independent from the graph and the spectral graph filter operates on a signal pointwise, this tells us

1. The polynomial is fixed once we find the coefficients $h_k$.
2. We can think of $\widehat{H(S)}$ as sampling values ${\lambda }_i$ along the curve $h(\lambda )=\sum _{k=0}^{K-1}{h}_k{\lambda }^k$.

Thus, changing the shift operator $S$ corresponds to a different set of points sampled from this polynomial.

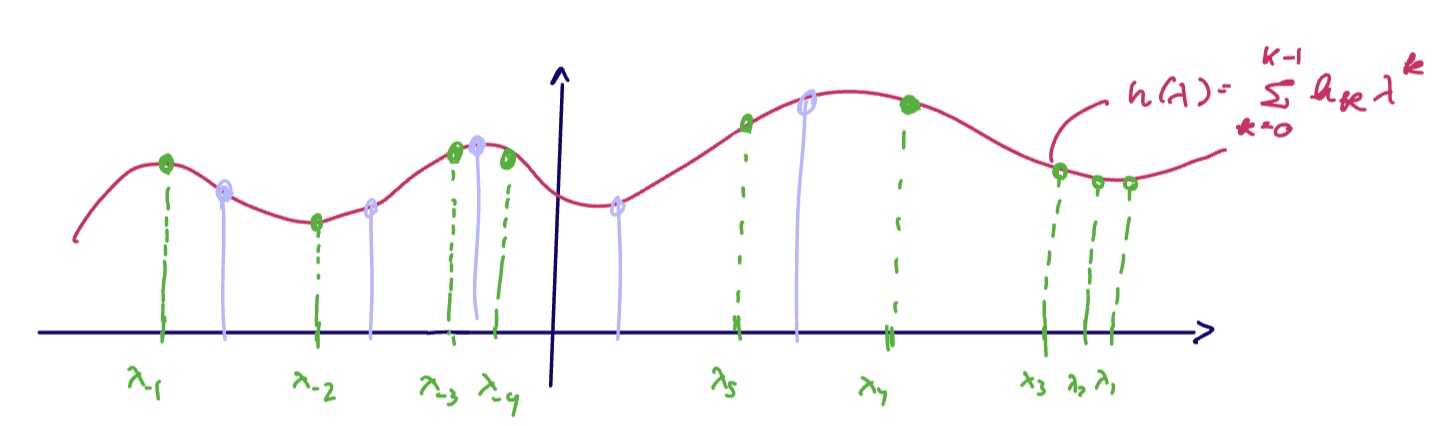
^spectral-as-poly

The graph fourier transform of the filtered signal is given as

For $(\ast )$, recall the definition of the inverse graph fourier transform.

1. the spectral representation of a graph filter is independent from the graph
2. the spectral graph filter operates on a signal pointwise