graph signal processing problem

Data

subject:: Data Science Methods for Large Scale Graphs
parent:: Graph Signals and Graph Signal Processing
theme:: math notes

Graph Signal Processing Problem

In a graph signal processing problem (or graph regression or signal regression), the graph $G$ is the data support, and is thus fixed. The data are graph signals $x \in R^{n}$ and we want to predict signals $y \in R^{n}$ . Assuming $x, y \sim p (x, y)$ , we regress signals $y$ on predictor signals $x$ .

Here, the hypothesis class are the graph convolutions $F$ $= {z = \sum_{k = 0}^{K - 1} h_{k} S^{k} x, h_{k} \in R}$

Our minimization problem is then $$\min_{h_{k}} \frac{1}{M}\sum_{j} \ell\left( y^{(j)}, \sum_{k=0}^{K-1}h_{k} S^k x^k \right)$$

Example

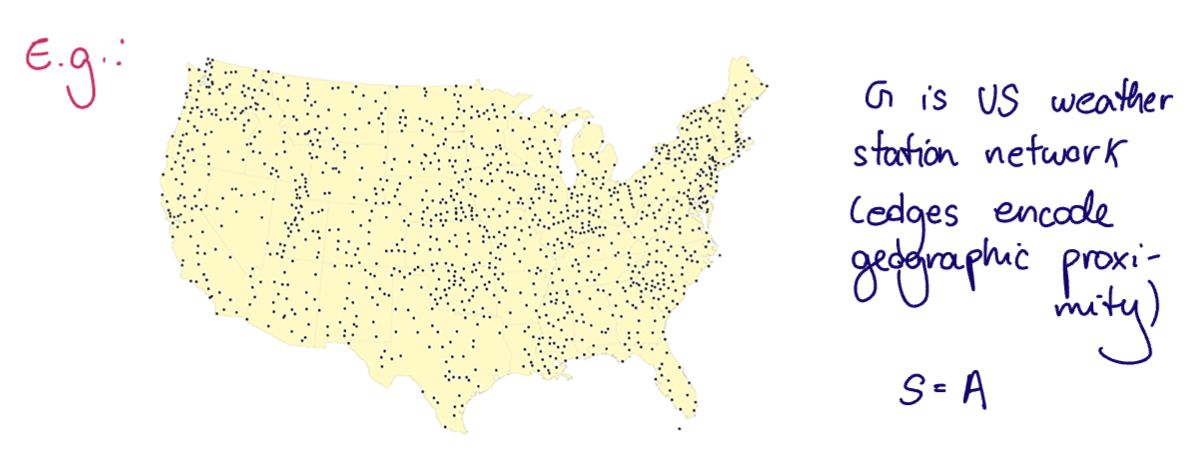
The fixed graph is the US weather station network. Suppose we have our $y$ , the recorded temperatures from February 3 from the last $n$ years, and our $x$ , the recorded temperatures from November 3 from the last $n$ years.

Temperatures on the graph are recorded as time series and
we want to predict the february temperatures from the november temperatures.

Application: temperature forecasting. Predict february 2026 temperatures $(y^{'})$ from the november 2025 temperatures $(x^{'})$ as

y^{'} \approx \sum_{k = 0}^{K - 1} h_{k}^{*} S^{k} x^{'}

Using $L^{2}$ loss, our minimization problem becomes:

min_{h_{k}} \frac{1}{M} \sum_{j} {| | y^{(j)} - \sum_{k = 0}^{K - 1} h_{k} S^{k} x^{k} | |}_{2}^{2}

Mentions

File
2025-02-03 graphs lecture 4