graph homomorphism

[[concept]]

Graph Homomorphism

Let $G = (V, E)$ and $F = (V^{'}, E^{'})$ . A graph homomorphism from $F$ to $G$ is a map $γ : F \to G$ such that

(i, j) \in E^{'} ⟹ (γ (i), γ (j)) \in E^{'}

ie, homomorphisms are adjacency-preserving maps (of $F$ ; the adjacency of $F$ must be preserved in $G$ .)
^definition

Exercise

How is a homomorphism not the same as a graph isomorphism?

Answer

Recall the definition of the isomorphism

Graph Isomorphism

Let $G$ and $G^{'}$ be two graphs. A graph isomorphism between $G$ and $G^{'}$ is a bijection $M : V (G) \to V (G^{'})$ such that for all $i, j \in V (G)$
$(i, j) \in E (G) ⟺ (M (i), M (j)) \in E (G^{'})$

The isomorphism requires that both graphs share all edges. The homomorphism requires that the second graph, $G$ , is a subgraph of the first, $F$ .

We also define

Homomorphism Count

We denote $hom (F, G)$ as the total number of homomorphisms from $F$ to $G$ .

Example

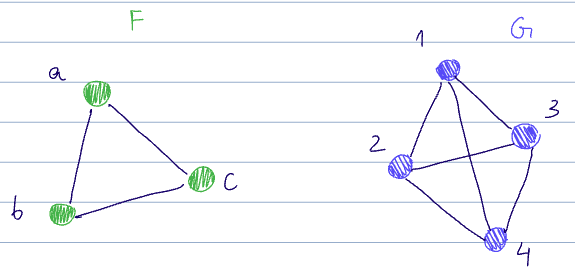
There are a few homomorphisms from $F$ to $G$ :

$(a, b, c) \mapsto (1, 2, 3)$
- And trivially, every permutation of $(a, b, c)$ is also a homomorphism here

There are also:

$(a, b, c) \mapsto (1, 2, 4)$
$(a, b, c) \mapsto (1, 3, 4)$
$(a, b, c) \mapsto (2, 3, 4)$
and for each of the above, each permutation of $(a, b, c)$ as well.

The homomorphism count $hom (F, G) = 24$ in this case.

Review

#flashcards/math/dsg

Q: How is an isomorphism different from a homomorphism?
-?-
A: The isomorphism requires that both graphs share all edges. The homomorphism requires that the second graph, $F$ , is a subgraph of the first, $G$ .

graph homomorphisms are {-adjacency-preserving maps-} (of $F$ in $G$ )

References

Mentions

File
graph automorphism
graph homomorphism
homomorphism density
2025-03-03 graphs lecture 11
2025-03-05 graphs lecture 12
2025-03-24 graphs lecture 14