GINs are maximally powerful for anonymous input graphs
[[concept]]
Takeaway
A GIN is a maximally powerful GNN in graph-level tasksfor anonymous inputs (ie
^statement
As long as we have an injective function from multisets to embeddings, we are able to distinguish between multisets.
We can then look at the graph level readout. In the original paper, this is defined at each layer as
Demonstration
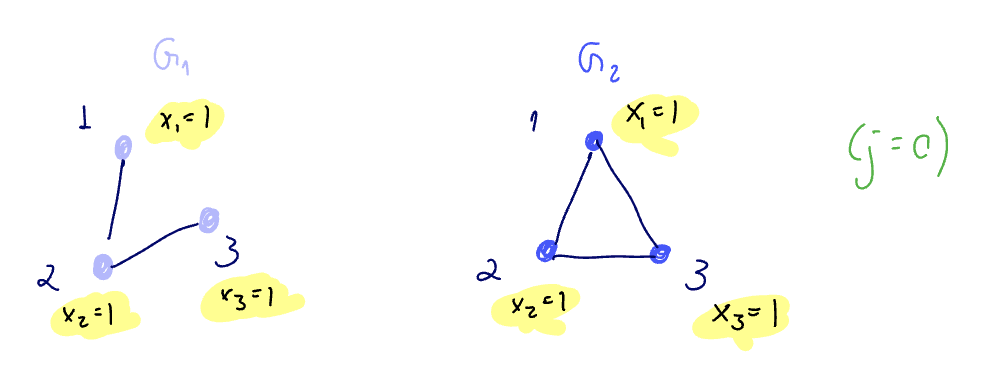
Can a GIN tell them apart? We assume
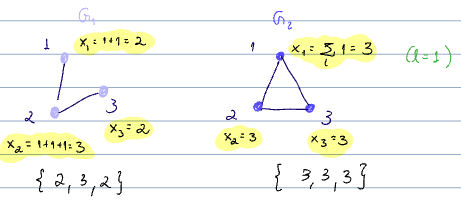
- output is
- readout is
- output is
- readout is