color refinement algorithm
[[concept]]
Color refinement algorithm
The color refinement algorithm is an algorithm to assign colorings to nodes.
Algorithm
Given graph
let
let
while True:
let
- assign colors based on previously assigned colors
if, break.else,
Here,
Example
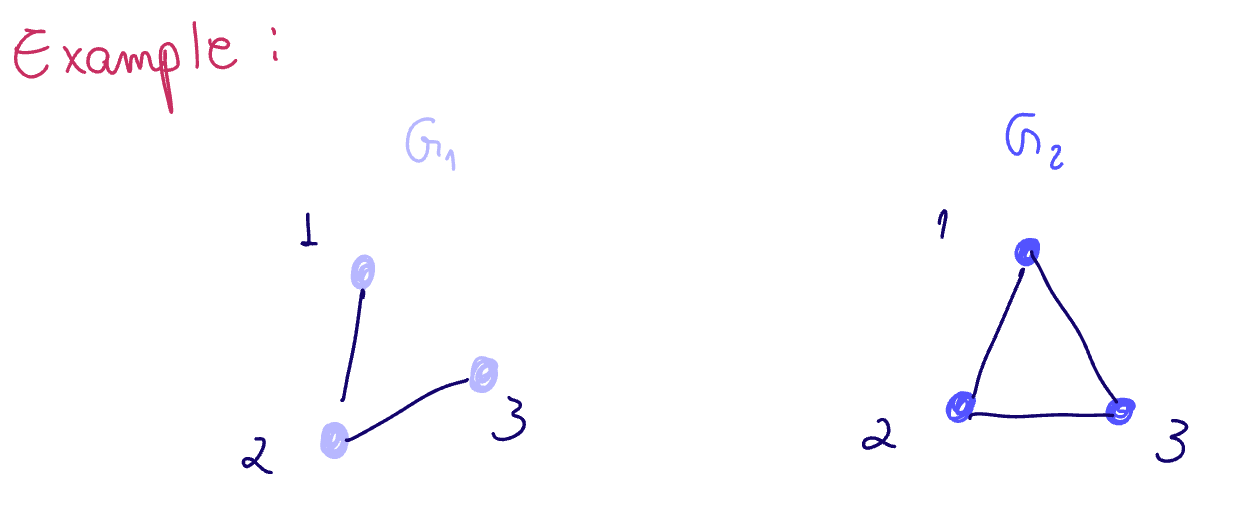
Color refinement for
No node features, so assume all 1. First, Assign colors based on node features.
step
step
Evaluate: did the colors change?
- Yes: continue!
step
Evaluate: did the colors change?
- No - so we are done!
- This is the final coloring.
return
Color refinement for
Again, there are no node features, so we assume the signals are all
step
step
evaluate: did the colors change?
- No - so we are done
- This is the final coloring
return